|
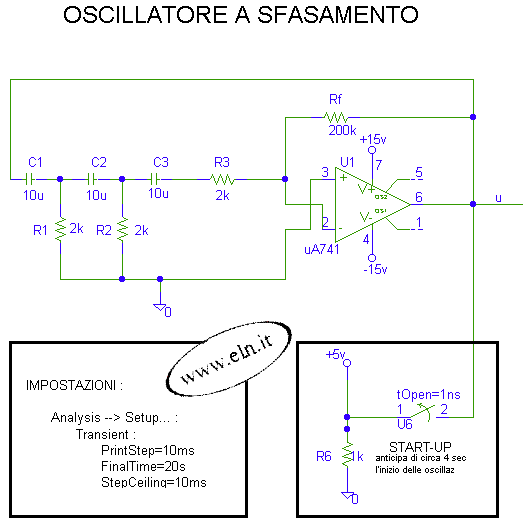
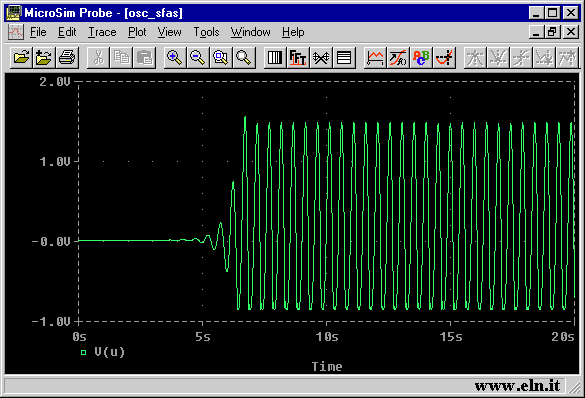
% OSCILLATORE A SFASAMENTO - www.eln.it
clear all; % cancella tutte le variabili & funzioni precedenti
clf; % cancella tutte le figure precedenti
% traccia il MODULO e la FASE di T :
% **********************************************************************************
w=logspace(-5,5,100); % vettore per diagr. mod & fase : 100 punti da 10^-5 a 10^5
p=w.*i;
f=2*pi;
Rf=200e3;
R=2e3;
C=10e-6;
A=-Rf/R;
H=(p*R*C).^3./((p*R*C).^3+6*(p*R*C).^2+5*(p*R*C)+1);
T=-H*A;
% ***********************************************************************************
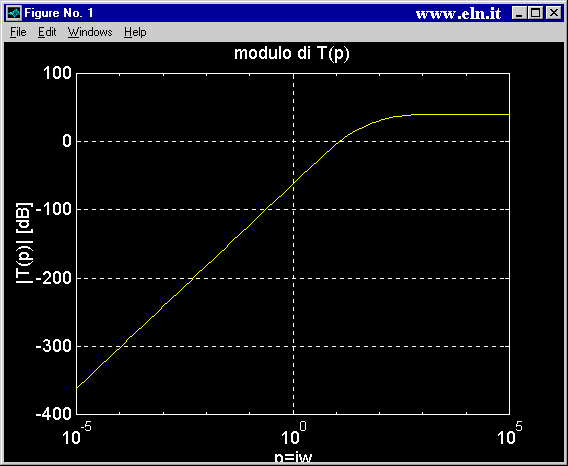
% disegna il modulo nella prima finestra
figure(1); % crea la finestra grafica
y=20*log10(abs(T)); % calcola il modulo della T in dB
semilogx(w,y,'y'); % traccia il grafico p,y di colore giallo con asse x in scala log e asse y in scala lineare
grid on; % mostra la griglia
zoom on; % attiva la T di zoom ( per cui cliccando su un punto del grafico, questo viene zoommato)
set(gca,'FontSize',14); % assegna al grafico corrente (gca) una dimensione del testo pari a 14
titolo=sprintf('modulo di T(p)');
title(titolo);
xlabel('p=jw');
ylabel('|T(p)| [dB]');
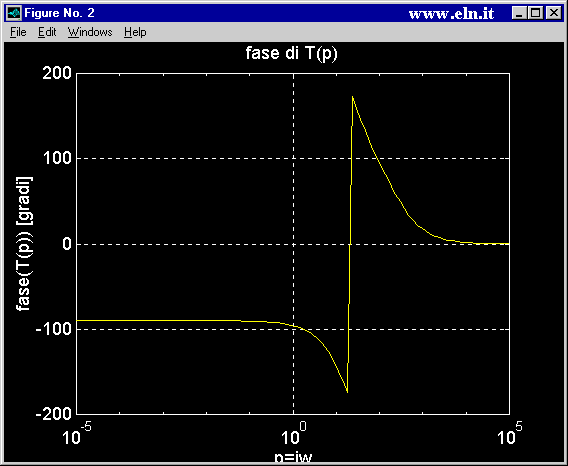
% disegna la fase nella seconda finestra
figure(2); % crea la finestra grafica
y=360/f*angle(T); % calcola la fase della T in gradi
semilogx(w,y,'y'); % traccia il grafico p,y di colore giallo con asse x in scala log e asse y in scala lineare
grid on; % mostra la griglia
zoom on; % attiva la T di zoom ( per cui cliccando su un punto del grafico, questo viene zoommato)
set(gca,'FontSize',14); % assegna al grafico corrente (gca) una dimensione del testo pari a 14
titolo=sprintf('fase di T(p)');
title(titolo);
xlabel('p=jw');
ylabel('fase(T(p)) [gradi]');
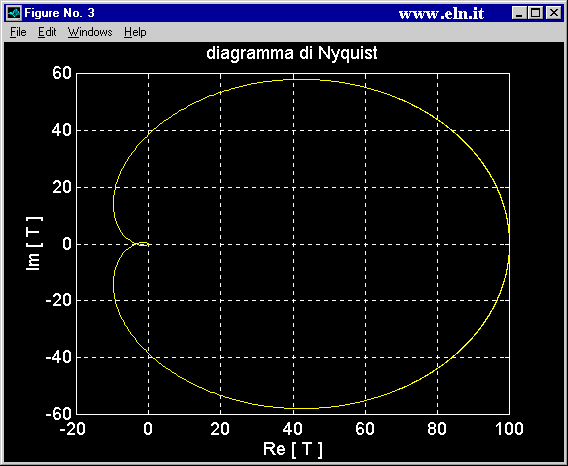
% traccia il DIAGRAMMA DI NYQUIST di T :
% ********************************************************************************
w=linspace(-1e4,1e4,1e4); % vettore per diagr. di Nyquist : 10000 punti da -10000 a +10000
p=w.*i;
f=2*pi;
Rf=200e3;
R=2e3;
C=10e-6;
A=-Rf/R;
H=(p*R*C).^3./((p*R*C).^3+6*(p*R*C).^2+5*(p*R*C)+1);
T=-H*A;
% ***********************************************************************************
% routine di tracciamento della curva
figure(3); % crea la finestra grafica
x=real(T);
y=imag(T);
plot(x,y,'y'); % traccia il grafico p,y di colore giallo con asse x in scala log e asse y in scala lineare
grid on; % mostra la griglia
zoom on; % attiva la funzione di zoom ( per cui cliccando su un punto del grafico, questo viene zoommato)
set(gca,'FontSize',14); % assegna al grafico corrente (gca) una dimensione del testo pari a 14
titolo=sprintf('diagramma di Nyquist');
title(titolo);
xlabel('Re [ T ]');
ylabel('Im [ T ]');
|

![]()
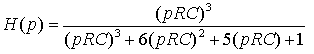
![]()